 | Píďalka 
23.10.2015 22:10
Bydliště: ČR
|
| FOTON
Dopplerův efekt světla
V momentě, kdy foton X vstupuje do oka pozorovatele A, zatímco se A blíží ke zdroji X, jenž je nehybný vůči gravitační síti, foton X nezbytně prodělá modrý posun v oku A, protože jeho rychlost se při přechodu, řekněme rohovkou, uzpůsobí atomární síti (prostředí) oka A a tím jeho rychlosti vůči fotonu X.1 Modrý posun fotonu X byl nutně způsoben jeho rozdílnou relativní rychlostí vůči oku A. Tím lze také vyjádřit stupeň modrého posunu fotonu součtem rychlostních vektorů fotonu X a protichůdného rychlostního vektoru oka pozorovatele A. Jednoduše řečeno, relativní rychlost pozorovatele A vůči fotonu X byla pozorovatelně vyšší než postulovaných Ajnštajnových 300,000 km/s a jen díky tomuto rychlostního rozdílu mohlo k posunu dojít. Bez něj by se Dopplerův posun definitivně nekonal.
Dopplerův efekt zvuku
Pozorovatel A sedí na střeše posledního vagónu vlaku a právě projíždí kolem šraněk, kde stojí pozorovatel B. I když je vzduch vzhledem k zemi nehybný, uhánějící píšťala pokládá skutečný kmitočet, řekněme 15 kHz, do relativně proudícího vzduchu, který zvuk píšťaly unáší, a tím natahuje vlnovou délku zvukové vlny za píšťalou. Tím se pozorovateli B jednak protáhne skutečný, celkový čas pískání píšťaly, řekněme ze skutečných 10 vteřin na řekněme 11 vteřin, a jednak slyší i nižší kmitočet pískání, řekněme 14 kHz, a ne skutečný kmitočet píšťaly 15 kHz. Z toho důvodu také B slyší i hlubší tón, než jakým se píšťala ve skutečnosti chvěje.
Toto je i princip červeného posunu spektrálních pásem světla Dopplerovým efektem v případě, že se zdroj světla vzdaluje od pozorovatele.
Pozorovatel A však slyší zvuk parní píšťaly lokomotivy jako vyšší tón oproti pozorovateli B. Pozorovatel A, právě projíždějící kolem šraněk, kde postává B, jede skutečně protaženým vlnám zvuku vstříc stejnou rychlostí, jakou od šraněk ujíždí píšťala. Díky tomu se mu také zkracuje skutečně natažená délka zvukových vln a tím také slyší délku pískání v jeho skutečné délce trvání 10 vteřin a tím také slyší i skutečný, originální kmitočet zvuku píšťaly 15 kHz. Ve skutečnosti se mu zvuk píšťaly, původně posunutý do červena (do hluboka) pohybem píšťaly nehybným vzduchem, posunul do modra díky jeho vlastnímu relativnímu pohybu vůči vzduchu stejnou rychlostí a směrem, jako se pohybuje vůči zemi píšťala. Posun do vysoka (modrý) se ovšem týče pouze té části zvukové vlny, se kterou přišlo ucho pozorovatele A do přímého styku. Zbytek skutečné zvukové vlny za píšťalou nebyl jeho pohybem nijak ovlivněn, jak dosvědčuje pozorování pozorovatele B.
Toto je i princip modrého posunu spektrálních pásem světla Dopplerovým efektem v případě, že se pozorovatel přibližuje ke zdroji světla.
Vlny zvuku kolem píšťaly lokomotivy, která se pohybuje prostředím, jmenovitě vzduchem, tvoří ve vzduchu vsazené, trojrozměrné ovoidy, v jejichž předním ohnisku se nachází píšťala. Tatáž geometrie šíření a spektrálních posunů platí i pro světlo, které se při pohybu gravitační sítí posunuje do modra před pohybujícím se zdrojem světla (píšťalou), a do červena za tímto zdrojem, zatímco kolmo ke směru pohybu zdroje a z místa zdroje se posunuje jen nepatrně do modra díky ovalitě šíření a pozici zdroje v předním ohnisku ovoidu. I tento posun záleží na jeho relativní rychlosti vzhledem ke gravitační síti, pokud není prostředím zároveň něco hmotného, co tvoří zmíněnou atomární síť magnetického řádu.2
Pokládá-li před sebe zdroj Y vlny do relativně se pohybujícího prostředí, jejich odraz od stejně rychle se pohybujícího zrcátka stejným směrem, zachytí detektor Z umístěný v pozici zdroje Y a se shodným vektorem pohybu s Y a Z jako nezměněný, ačkoliv tato vlna projde čtyřmi Dopplerovými posuny. K prvnímu posunu do modra dochází při pokládání vln zdrojem, ke druhému, červenému dojde při dopadu vln na zrcátko, ke třetímu a opět červenému dojde při odrazu vln od zrcátka a ke čtvrtému posunu do modra dojde při zachycení vln detektorem. Výsledek na detektoru Z je tudíž vždy stejná vlnová délka a kmitočet jako na zdroji Y. U světla se tímto nelze dožadovat, aby u něj došlo na detektoru Z ke spektrálnímu posunu tímto způsobem.
Z toho vyplývá, že modrý posun fotonů míjejících Ajnštajnova 'magického pozorovatele, které dotyčný pozorovatel fyzicky neopůsobil, je pouhou iluzí, pokud by to bylo vůbec nějakým způsobem možno zjistit. Na straně druhé, rychlostní složka vektoru světla je prvotně závislá na hmotném prostředí a druhotně na částicovém prostředí gravitační sítě. Jeho rychlost v gravitační síti je pak dána i lokálním napětím sítě a její hustotou. Lze ji tudíž jen velice zhruba považovat za konstantní rychlost i ve vakuu.
Vlna nebo částice?
Pokud by mělo světlo vyzařovat jako série soustředných kulových vln, bylo by nutně tlakovou vlnou v prostředí, tudíž podélným vlněním, stejně jako zvuk, a ne příčným. Jenže potom jaké částice, zvané fotony? No a kde je nějaké prostředí ve vakuu, pokud jím není sama radiační síť tvořená gravitačním zářením, tedy jakýsi ether? Avšak, i kdyby byla gravitace takovým etherem, jak to přijde, že dvouštěrbinový pokus Thomase Younga vykazuje jakýsi vzor, prý vzájemné interference (rušení) bílého, a tím mnohafrekvenčního, světelného paprsku slunce? Jak již zmíněno, Youngův dvouštěrbinový pokus byl proveden pomocí dřevěné destičky, ve které byla nastojato vyříznuta obdélníková díra a zhruba do delší osy díry byl opět nastojato vložen železný hřebík (Kdysi dohledatelné na netu). Bylo použito sluneční světlo ze štěrbiny na zatemněném okně.
Nejdříve se snad podívejme, co je špatně s vysvětlováním tohoto pokusu, s jeho filosofií a s různými analogiemi:
 V první řadě se dnes setkáváme na netu téměř výlučně s demonstracemi pomocí jednofrekvenčního (monochromatického) světla a se schémátky. Skutečných fotografií výsledků, a to provedených s dením světlem, se dnes jaksi nedostává. Proč?
Protože dvouštěrbinový lom světla na typickém schématu (obr. 6) je ukázán, jak by se přibližně jevil na vodní hladině za použití jedinné vlnové délky a frekvence. Totéž pak ukazuje skutečné foto (obr. 7) vodní hladiny se dvěma seriemi jednofrekvenčních vln, vyvolaných oscilací dvou koulí ve vodě. Jenže, tohle nejde provést s vlnami, které jsou mnohafrekvenční a o různých vlnových délkách, výškách a tím i rychlostech a frekvencích. Někdo nám tu záležitost velice idealizuje, vnucuje nám své zavádějící doměnky a vyvolává v nás falešné představy, že takhle to je.
Protože někdo nemá zájem nám ukazovat něco, co se mu nehodí do krámu, a to, že pokus provedený s denním světlem ukazuje lom světla do překrývajících se barevných pruhů, popřípadě fleků duhy spektrálního rozkladu (dle provedení štěrbin), který nám stejně tak ukazuje i optický hranol, mřížka, anebo čočka. (Obr. 8) je klikací odkaz na zajímavé video pokusů s dením světlem, prý od amatéra (anglina). Je dostatečně názorný i bez zvuku na to, aby si ho mohl kdokoliv sám zopakovat a ověřit. https://www.youtube.com/watch?v=wQTVcaA3PQw
Protože v tom videu dotyčný dokonce ve tmavé komoře použil jenom "hřebík", bez jakékoliv štěrbinové přepážky, a výsledek lomového, barevného vzoru je stejný a někdo to zatra dobře ví. Píchněte si do vody kolík a podívejte se, co udělá s jakýmikoliv vlnami, a jestli dostanete vzor podobný tomu, co ukazují pečlivě provedené pokusy se štěrbinami. Bývaly na netu i další fotky poukazující na různé vzory lomu denního světla dvouštěrbinovým pokusem, podle toho, jak byl pokus sestaven, zvláště pak zda byly použity jen kulaté dirky, nebo "hřebík", ale vždy s duhovým lomem. Obraz na matnici často vypadá jako duhováná spirála, od středu levotočivá na jednu stranu a pravotočivá na druhou.
Protože celý slavný Youngův pokus se světlem má další zásadní, i když málo zmiňovaný problém. Pokud není středová přepážka štěrbin, tedy náš "hřebík", dostatečně úzká, pokus se světlem nefunguje, zatímco vodní pokus funguje s jakkoliv tlustou středovou přepážkou a je jen otázkou délky hladiny za štěrbinovou přepážkou, kdy se ukáže.
Protože to, co se děje na světelné matnici pokusu, odporuje tomu, co se děje na vodní matnici pokusu, a to i s prakticky jednofrekvenčními vodními vlnami. Žádný z vodních experimentů se totiž nezabývá tím, jaký výsledek se ukazuje na vodní matnici, tedy řekněme na přístavní zdi. Dovolil jsem si tedy takový pokus spáchat sám, protože jsem se na vodě vyskytoval hodně a pozoroval, a i bez pokusu mi bylo jasné, co dostanu na matnici, a protože je celkem nenáročný. Viz popis níže.
Protože s platností, či neplatností interpretace dvouštěrbinového pokusu, který jak vidno ani nemusí být dvouštěrbinový, stojí a padá celá filosofie a platnost kvantové mechaniky se všemi jejími zázraky, na kteréžto se dobře živí mnoho učených kazatelů předepsané pravdy.
Ne, že bych se nějak klonil ke grafickému vyjádření teorie šíření a struktury elektromagnetického záření, či jeho teoretickému výkladu, nicméně grafické schéma (obr. 9) poukazuje na nepoužitelnost vodní analogie i v rámci ortodoxních vysvětlování, nebo obráceně, o nepoužitelnosti teoretických vývodů elektromagnetického vyžařování. Jde o vnitrorganizační, ortodoxní paradox.
Co se týče vodní analogie, vlny na hladině se mohou šířit ze společného bodu podél rozhraní dvou látek, vody a vzduchu, kdy je hladina pod gravitačním pnutím a pnutím způsobeným atmosferickým tlakem. V měřítku oceánu příliš nezáleží na tom, zda jde o rozhraní vyloženě ploché, či mírně zakřivené. Definitivně se však tyto vlny nešíří ani dolů, nebo nahoru, i když mají svou prostorovou dynamiku i pod hladinou. Tlakové vlnění v látce, řekněme zvuk ve vzduchu, možná i ztrácí na intenzitě se čtvercem vzdálenosti, avšak světlo, pokud má být částicové, ji může ztrácet jedinně díky řídnutí radiace fotonů. Zda je částicové je však také otázkou, ale zatím mi nezbývá, než o něm takto uvažovat.
Pokračování
 | 
Obr. 6 (typické školní schema)
(Dostupné jen pro přihlášené uživatele fóra)
Obr. 7 (fotka vodní interference)
(Dostupné jen pro přihlášené uživatele fóra)
Obr. 8 (fotka interference deního světla)
(Dostupné jen pro přihlášené uživatele fóra)
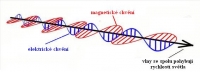
Obr. 9 (schema Maxwel elektromag. vlna)
(Dostupné jen pro přihlášené uživatele fóra)
Obrázky není povoleno jakkoli šířit bez souhlasu jejich autora, a to ani v jakékoli upravené formě
|
|
|
Podpořte chod fóra 