Omfórum

Hlavní přehled | Info a nápověda

Přihlásit | Registrovat

Příspěvek umístěný v tematickém vlákně: TTG - Teslův toroidní generátor (str. 2)

Adam

02.01.2018 15:00
Bydliště: Praha

6149

576

5989

Jarin's napsal(a): Ještě mě napadlo z jakého rozsahu úhlu α vychází při počítání toho Φ = B*S*COS(α). Jestli se nemůže stát, že se výsledné Φ tím COS() otočí, zatímco B zůstává stejné. ...

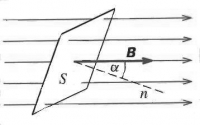
Φ = B*S*Cos(α) je obecný vztah, který pomocí součinitele Cos(α) ošetřuje možnost, že by rovina vyšetřovaného Φ nebyla kolmá na směr B a pomocí tohoto cosinu se najde správná "složka" B, kolmá na vyšetřovanou rovinu. S tím souvisí první obrázek.

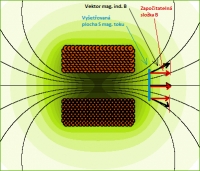
Nebo se to používá ještě k příbuznému účelu, že vyšetřujeme Φ v rovině, kterou sice chceme mít zcela kolmou na působení B, ale některé vektory B kolmo do této roviny nevstupují - vstupují šikmo, takže pro získání korektního celkového Φ musíme u těchto šikmých vektorů B dopočítat vhodnou složku B opět danou "úhlem odchýlení". Viz. druhý obrázek.

Úhel α tedy vždy řeší pouze částečné odchýlení. Tok Φ je "plošný součet" hodnot B v jednom určitém směru, tedy protisměrně to skutečně jít nemůže. Jedině, pokud bys zobrazoval jen nějaký unikátní dílčí vektor B, který jako jeden z mála zrovna někde jde protisměrně, ale ostatní B důrazně prosadí jiný směr. Skutečně to tedy nedává smysl, proč to ten program uvádí takto, jako kdyby vlastně vyšetřoval dvě úplně jiná místa v tom Tvém modelu.

Ale víš co? Aby toho nebylo málo, tak ještě než se pustím do křivky napětí, měli bychom nějak vyřešit, že sice určitě chci vycházet z křivky Φ, ale ta červená křivka ve Tvém posledním grafu (údajná hodnota mag. ind. B) mi přijde daleko realističtější, než ta modrá křivka Φ.